第三種電気主任技術者（電験三種） 過去問
令和7年度（2025年）上期
問3 (理論 問3)
問題文
図のように、環状鉄心に二つのコイルが巻かれている。コイル1の巻数はNであり、その自己インダクタンスはL［H］である。コイル2の巻数はnであり、その自己インダクタンスは9L［H］である。巻数nの値を表す式として、正しいものを次の選択肢のうちから一つ選べ。
ただし、鉄心は均一で一定断面積をもち、コイル及び鉄心の漏れ磁束はなく、鉄心の磁気飽和もないものとする。
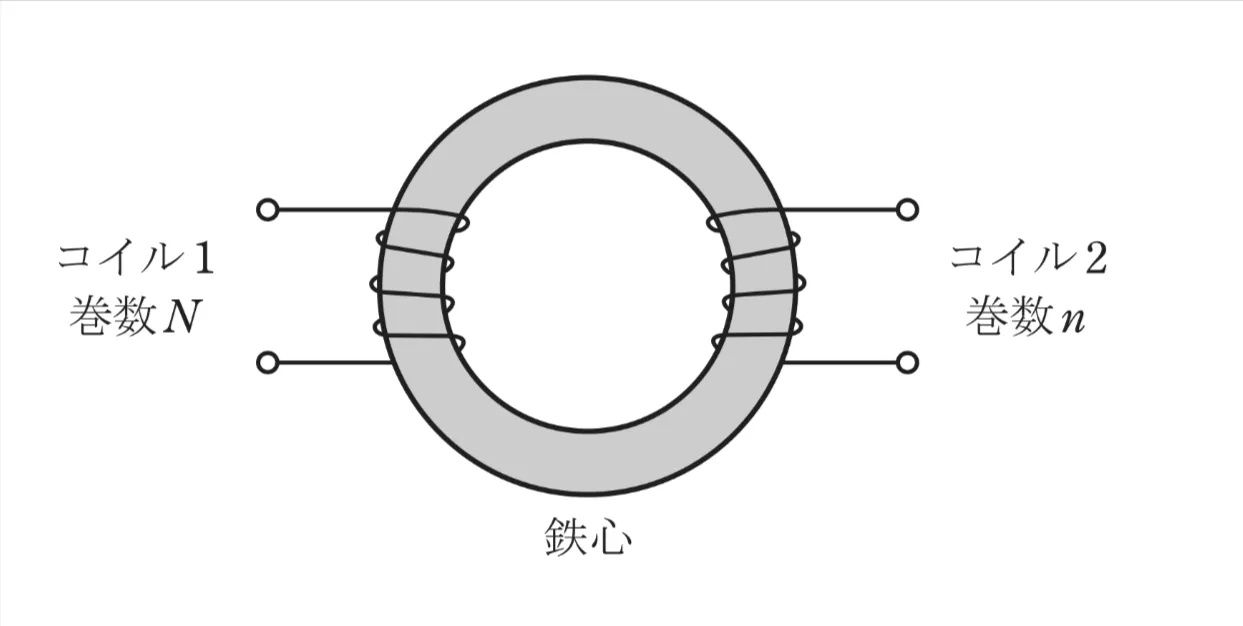
ただし、鉄心は均一で一定断面積をもち、コイル及び鉄心の漏れ磁束はなく、鉄心の磁気飽和もないものとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
第三種電気主任技術者（電験三種）試験 令和7年度（2025年）上期 問3（理論 問3） （訂正依頼・報告はこちら）
図のように、環状鉄心に二つのコイルが巻かれている。コイル1の巻数はNであり、その自己インダクタンスはL［H］である。コイル2の巻数はnであり、その自己インダクタンスは9L［H］である。巻数nの値を表す式として、正しいものを次の選択肢のうちから一つ選べ。
ただし、鉄心は均一で一定断面積をもち、コイル及び鉄心の漏れ磁束はなく、鉄心の磁気飽和もないものとする。
ただし、鉄心は均一で一定断面積をもち、コイル及び鉄心の漏れ磁束はなく、鉄心の磁気飽和もないものとする。
- N／9
- N／3
- 3N
- 9N
- 81N
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
鉄心付きコイルの自己インダクタンス L［H］は、次式で表されます。
L=N2/R
N はコイルの巻数、 R は鉄心の磁気抵抗です。
この問題では鉄心は均一で一定断面積を持ち
漏れ磁束や磁気飽和がないとされているため
2つのコイルで磁気抵抗は同一と考えることができます。
したがって、自己インダクタンスは巻数の2乗に比例します。
この関係を用いて巻数 n を求めます。
自己インダクタンスは巻数の2乗に比例するため
巻数が小さくなると自己インダクタンスも小さくなります。
しかしこの問題では、コイル2の自己インダクタンスはコイル1の9倍であるため
巻数が N/9 のように小さくなることはありません。
よって、この選択肢は誤りです。
自己インダクタンスが9倍になるためには
巻数は √9 =3 倍になる必要があります。
巻数が N/3 では自己インダクタンスは 1/9 倍となってしまい条件を満たしません。
したがって、この選択肢は誤りです。
コイル1の自己インダクタンスを L、巻数を N とすると
L ∝N2
コイル2の自己インダクタンスは 9L であるため
9L/L=n2/N2 より 9=n2/N2 となります。
これを解くと n=3N となります。
したがって、この選択肢が正しいです。
巻数が 9N の場合、自己インダクタンスは巻数の2乗に比例するため
(9N)2=81N2
となり、自己インダクタンスは81倍になります。
これは条件の9倍と一致しません。
よって、この選択肢は誤りです。
巻数が 81N の場合、自己インダクタンスは
(81N)2
に比例し、極めて大きな値となります。
この問題の条件である自己インダクタンス9倍とは全く一致しません。
したがって、この選択肢は誤りです。
参考になった数23
この解説の修正を提案する
02
環状鉄心にある二つのコイルの巻線の巻数を求める問題です。
ただし書きから、鉄心は均一で、一定断面積、漏れ磁束がない、磁気飽和もないとされてますので、すべて一定と考えます。
自己インダクタンスLは、L₌μSN２/ｌで求まります。
よって、μ、S、ｌは一定になっていますので、ＬとＮだけで考えます。
コイル１では巻数Ｎで、自己インダクタンスはＬ、コイル２ではｎとなり、自己インダクタンスは９Ｌとなっていますので、
巻数ｎについて自己インダクタンスに関してまとめると、（Ｎ／ｎ）2₌Ｌ/9Ｌにあり、
ｎ=3Ｎとなります。
誤：求めた値と異なります。
誤：求めた値と異なります。
正：求めた値と合致します。
誤：求めた値と異なります。
誤：求めた値と異なります。
環状鉄心のコイルの巻線に関する問題でした。
与えられた値が何を指しているかを理解できれば、解答が見えてくると思います。
参考になった数3
この解説の修正を提案する
前の問題（問2）へ
令和7年度（2025年）上期 問題一覧
次の問題（問4）へ